Teorema de Pitágoras
El teorema de Pitágoras se le atribuye al filósofo y matemático griego Pitágoras de Samos y su escuela llamada Los Pitagóricos, aunque no se tiene certeza de ello pues se tienen pruebas que los babilonios ya conocían ternas de números “especiales” (hoy en día llamadas ternas pitagóricas) ¡al menos un milenio antes! Parece ser que Pitágoras y Tales se conocieron al punto de ser el primero discípulo del segundo.
Aquí es donde entra el famoso caso del teorema de Pitágoras. Este teorema establece la relación entre los lados de un triángulo rectángulo. El teorema afirma que el cuadrado de la hipotenusa (siendo ésta el lado más largo del triángulo) es igual a la suma de los cuadrados de los catetos (siendo éstos los lados más cortos que forman el ángulo rectángulo). Este teorema ha aportado numerosos recursos prácticos en antiguas civilizaciones griegas y anteriores como lo son la egipcia y babilónica. Sin embargo, es a Pitágoras quien se le atribuye la primera demostración válida del teorema.
Gracias a ello, la escuela tuvo numerosos avances. La generalidad de este teorema matemático hacía cumplir la purificación y la perfección del alma ya que aumentaba ese conocimiento en la persona. Además, ayudaba a conocer el mundo como armonía. El universo era considerado como un cosmos. El cosmos no es más que un conjunto ordenado en el que los cuerpos celestes guardan una posición en la que están en completa armonía. Las distancias entre cada cuerpo celeste tienen proporciones similares y es correspondiente a los intervalos de la octava musical. Para este matemático, las esferas celestes giraban y producían lo que se denominaba música de las esferas. Esta música no se puede escuchar por el oído humano ya que es algo permanente y perpetuo.
Ejemplo 1:
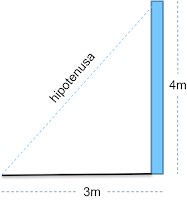
Para evitar que se caiga la carpa del jardín, Rocío debe colocar un cable de acero en un poste que lo sostenga. Si el poste mide 4 m de altura y el cable debe estar separado a 3 m de la base del poste. ¿Cuánto cable debe comprar?
Podemos observar que se forma un triángulo rectángulo donde se conoce el valor de los dos catetos que forman el ángulo recto y se desconoce el valor de la hipotenusa (longitud del cable) por lo que usaremos el teorema de Pitágoras y lo sustituiremos con los datos con los que contamos.
Solución
c² = a² + b²
c² = 3² + 4²
c² = 25
c = √25
c = 5 La longitud del cable es de 5 metros
Ejemplo 2:
Los fabricantes de pantallas de TV clasifican sus modelos por la longitud de la diagonal de su producto. En la categoría de 40 pulgadas se disponen modelos de 34 pulgadas de largo, ¿cuánto miden aproximadamente de ancho?
Podemos observar que se forman dos triángulos rectángulos iguales de los que se conoce el valor de la diagonal (hipotenusa) y uno de los dos catetos que forman el ángulo recto; y se desconoce el valor del otro cateto (ancho de la TV) por lo que usaremos el teorema de Pitágoras y lo sustituiremos con los datos con los que contamos.
c² = a² + b²
40² = 34² + b²
1600 = 1156 + b²
1600 - 1156 = b²
444 = b²
√444 = b
b = 21.07
¡Ahora te toca a ti!
Debido a los fuertes vientos, es necesario fijar un poste con tres cables de 8 m cada uno y atarlos al suelo a una distancia de 6 m de la base.
¿A qué altura se tendrán que fijar los cables en el poste?
Juan trabaja en una carpintería. Le llevaron a reparar una mesa cuadrada que tiene una abertura justo en su diagonal. Para repararla decide colocarle un soporte de madera. ¿Cuánto debe medir el soporte si el área de la mesa es de 9 m2?

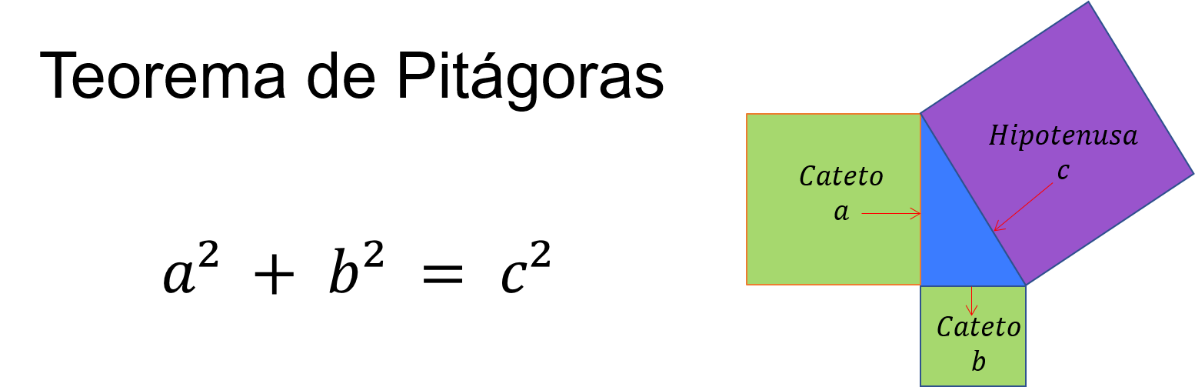



Hola Maestro, es un gusto poder saludarle y enviarle por este medio un reconocimiento al mérito de su trabajo. Pese a no dominar la materia de matemáticas, la forma en como ha diseñado su Blog me resultó de fácil de entender. ¡Saludos!
ResponderEliminarHola profesor, me parecio muy interesantes las actividades, pero en lo personal el video me hubiera gustado verlo antes de los ejemplos, para tenerlo màs claro, pero de cualquier manera considero que la inofrmaciòn presentada explica el tema.
ResponderEliminar